Algorithm Design – what else!
August 1, 2019
In diesem Beitrag bin ich der Frage «Was ist ein Algorithmus und wofür setze ich ihn wie ein» auf der Spur. Bald war mir klar: Um einen Algorithmus anzuwenden, braucht es ein Problem, das man damit lösen kann. Die beste technische Erklärung, die es aus Sicht unseres Dozenten dafür gibt: «Formalized steps to solve a problem».
Ein nicht repräsentatives Anschauungsbeispiel für diese Defintion ist ein IKEA-Bauplan: Je formaler der Bauplan, desto besser.
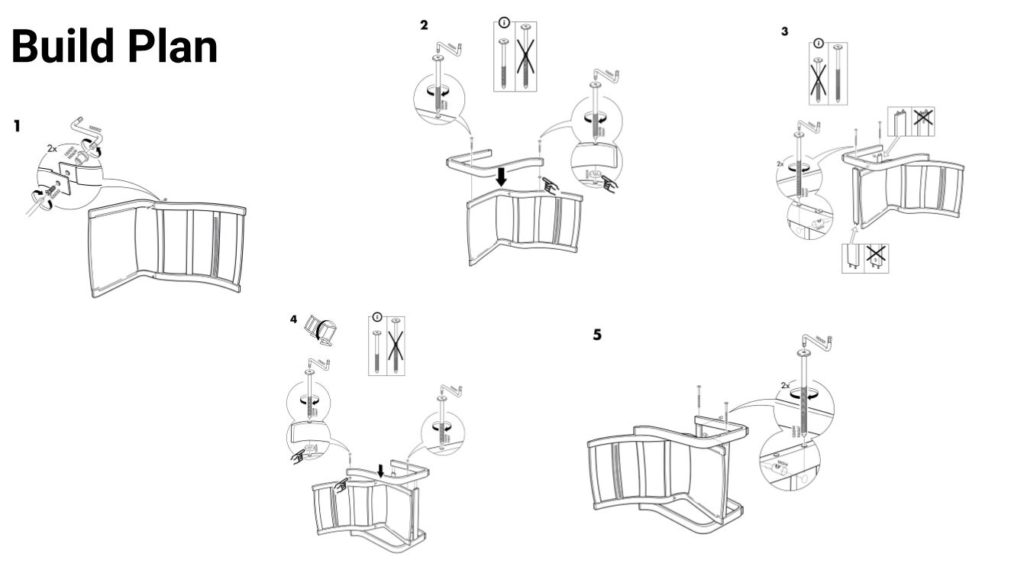
Bei diesem Beispiel ist jedoch nicht die Maschine, sondern ein Mensch der/die Ausführende. In der Regel sind das jedoch Maschinen, die einen Algorithmus ausführen.
Am Bespiel eines digitalen Kochrezepts sehen wir auch gleich, welche Parameter bei der Berechnung sich verändern können:
d.h. es gilt bei der Anwendung eines Algorithmus, sich zu überlegen, welche Parameter sich verändern können.
Mögliche Ziele für den Einsatz eines Algorithmus sind bspw.:
Ein bekannter Optimierungs-Algorithmus ist der sogenannte «Needle-in-a-Haystak–Algorithm». Ziel ist es den Input mit der Lösung zu vergleichen. Ergebnis = anzustrebender Score
Beim Optimierungs-Algorithmus kann wie folgt vorgegangen werden
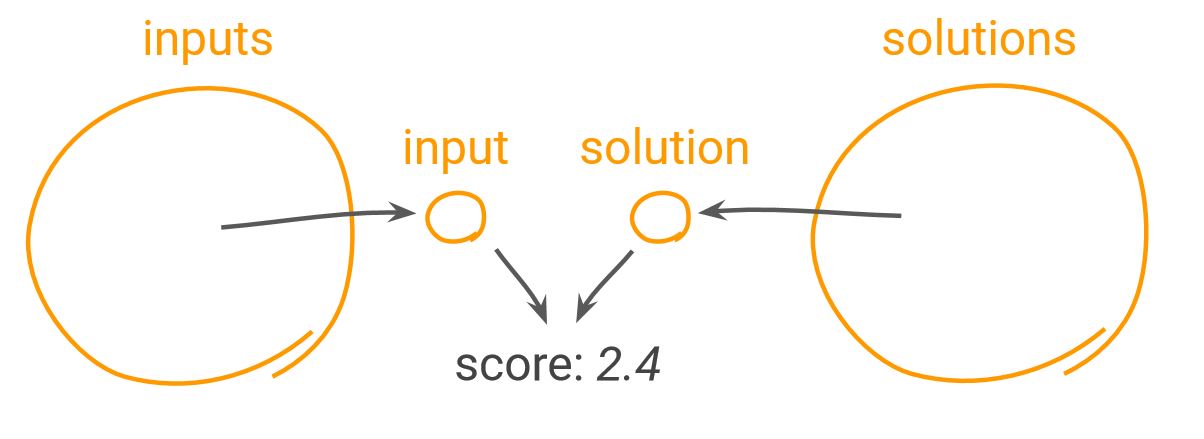
Als Beispiel diente wiederum die Verpflegung von Gästen (ähnlich zum vorgängigen Kochrezept):
Problem:
Wir laden zu einem Dinner ein und es gibt die Möglichkeit, dass ein Gast nicht satt werden könnte
Input:
Es sind 5 Gäste eingeladen.
Lösung (Modell):
Genügend Produkte (Zutaten) einkaufen und verarbeiten.
Score:
Sind alle Gäste zufrieden und satt geworden. Wie viel Essen ist übrig geblieben.
–> Die Scoring-Funktion gibt also formal an, wie gut die Lösung zum Input passt
(Messkriterium, KPI)
Als weiteres Beispiel wurde «Automated Trading» besprochen:
| Problem | Automatisiertes Trading |
| Input | stock history |
| Lösung | schedule of sell/buy |
| Score | earned money |
Auch im Machine-Learning kann diese Analyse angewendet werden:
Inuput Testdaten von Tierbildern
Lösung Die Katzenbilder sollen identifiziert werden
Score Wie hoch ist der prozentuale Anteil der richtig identifizierten Katzenbilder
Zu diesem Beispiel wurde der Begriff Cross Entropy erläutert. Ein Begriff aus der mathematischen Statistk, um die Qualität eines Modells für die Wahrscheinlichkeitsverteilung zu messen.
Oder angewendet für unser Beispiel:

Der einfachste Algorithmus um eine Lösung zu finden ist «Brute Force». Dabei gilt es alle Lösungen durchprobieren, um zu sehen, welche Lösung die beste ist. Eine Lösung nach der andern wird getestet, bis die beste übrigbleibt.
Brute Force ist immer dann ein guter Ansatz, wenn man nicht weiss wie man es eigentlich machen könnte. Es liegt aber auf der Hand, dass dieser Ansatz vergleichsweise ineffizient ist.
Folgende drei Methoden wurden zusätzlich besprochen:
| Greedy | Lösung wird iterativ aufgebaut, indem immer wieder der nächst beste Teil dazu integriert wird (bspw. Travel Salesman). |
| Local Search | Es wird mit einer spezifischen Lösung gestartet. Diese wird anschliessend iterativ verbessert (Fit Algorithmen). |
| Dynamic Programming | Es werden kleine Teillösungen gebaut. Diese Teillösungen werden anschliessend zu einer Gesamtlösung zusammengebaut |
A) Vernünftige Lösungszeit – unabhängig der # Inputs
B) Vernünftige Speichergrösse (RAM) – unabhängig der # Inputs (deshalb ist ein rekursiver Algorithmus nicht geeignet).
C) Er ist einfach zu implementieren
Im letzten Teil haben wir uns mit zwei Gliederungsmöglichkeiten des Algorithmus beschäftigt:
Problem Eine Menge von Zahlen müssen sortiert werden.
Eingabe Eine Folge von n Zahlen
Lösung Alle Permutationen dieser Zahlen
Score Wie viele Zahlen sind in der richtigen Reihenfolge
Wie sortiert ein Computer, damit ich die gesuchte Information schnellst möglich und in der gewünschten Qualität erhalte? Und welchen Algorithmus wendet er an?
Um diesen Fragen auf den Grund zugehen haben wir die verschiedenen Möglichkeiten in Form eines «Becherspiels» angewendet:
Auf dem Tisch stehen 10 Becher, durchnummeriert und markiert von 1 bis 10. Die Reihenfolge ist unsortiert.
Ziel ist es, die Becher mit möglichst wenig Schritten (und in möglichst kurzer Zeit) in die Richtige Reihenfolge zu bringen: Von links 1 bis rechts 10.
Execution time:
Best case benötige ich dafür n = 10 Schritte
worst case benötige ich dafür n2 Schritte = 100 Schritte
Besser – und in diesem Fall der average case – wäre, wenn ich immer zwei Becher herausziehe und in zwei Teile clustere (Binary Tree).
Ist n nicht bekannt, so sollte die Randomisierung (Zufallseinteilung) angewendet werden.
Best case ich benötige dafür mindestens «n» Schritte (n2)
average case n-log2(n) – die Maschine zieht immer zwei Daten heraus und sortiert in zwei Teile (Binary Tree)
Kennen wir bspw. aus einem dem Anwendungsfeld «Staffing von Projektteams». Dabei soll eine Person einem bestimmten Projekt zugewiesen werden. Es gilt, vorgängig zu bestimmen, welche Zuweisung aufgrund welcher Kriterien sinnvoll ist:
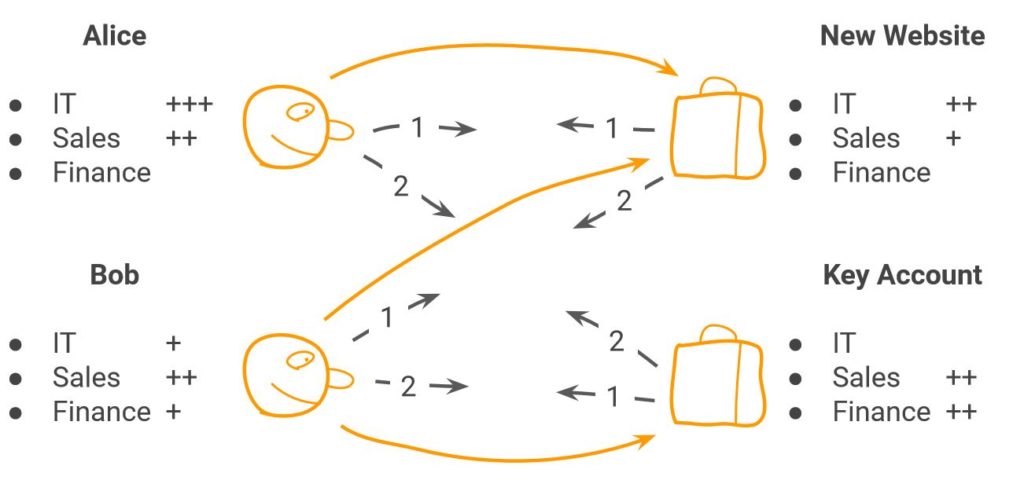
Zu 1.) David Gale und Lloyd Shapley haben in den 60er Jahren bewiesen, dass es möglich ist ein SMP «Stabiles Matching Problem» anhand des «Gale-Shapley-Algorithmus» zu lösen, indem sie die Zuordnung mit einem verzögerten Akzeptanzalgorithmus erstellen. Dieser wird in einem iterativen Prozess angewendet – das heisst, er entspricht dem vorgängig beschriebenen Greedy-Ansatz.
Die Herren Lloyd S. Shapley und Albert E Roth haben für diese Theorie der stabilen Allokation 2012 den Nobelpreis für Wirtschaftswissenschaft erhalten.
Dieser Algorithmus kann nebst Projektstaffing bspw. auch bei der Partnervermittlung oder bei der Studententenzuordnung für Universitäten eingesetzt werden.
Zu 2.) Insbesondere die Variante «Wahl der Mitarbeitenden» könnte jedoch ein unstabiles Matching zur Folge haben: Jemand ist unzufrieden, weil sein Wunsch nicht erfüllt wurde, ein anderer hat zwar seine Wunschzuordnung erhalten, ist damit jedoch überfordert.
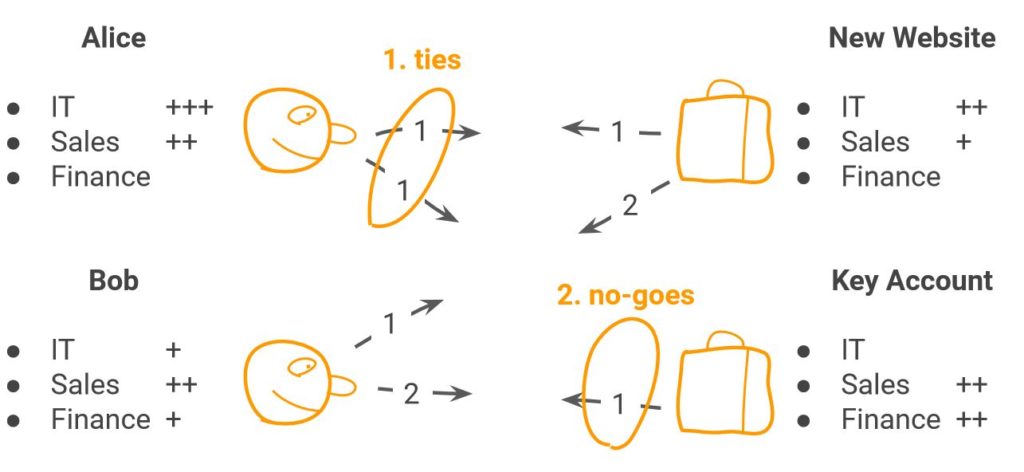
Die Kombination von «ties» und «no goes» hat denn auch zur Folge, dass der Gayle Shapley Algorithmus nicht anwendbar ist.
Zu 3.) Um die Zuweisung von Mitarbeitern auf Basis Wirtschaftlichkeit vorzunehmen, haben wir zum Abschluss des Nachmittags eine letzte Challenge erhalten:
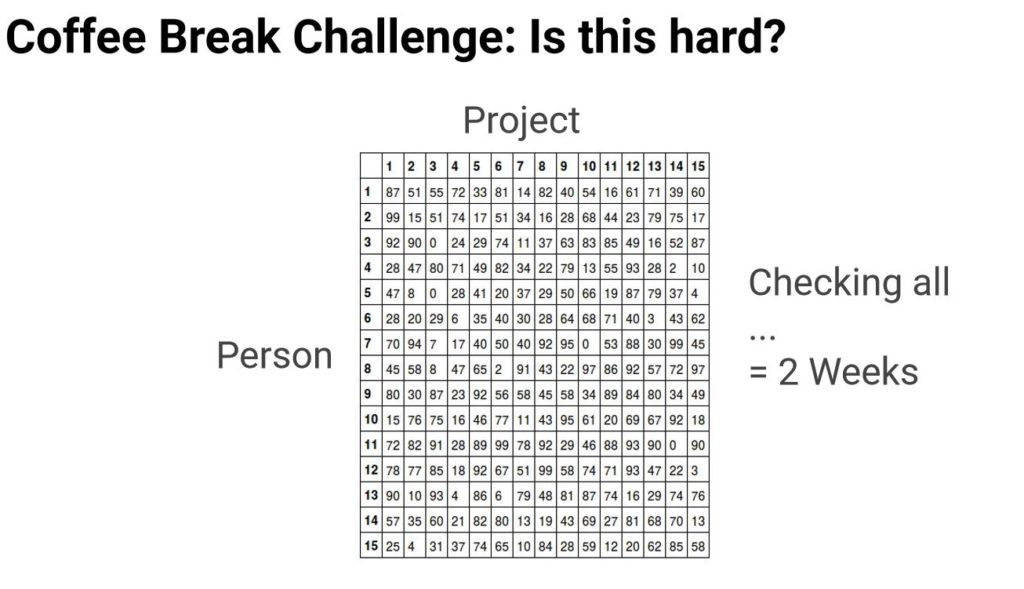
Hier sind auch Sie als Leserin und Leser aufgefordert, ihr neu erworbenes Wissen einzusetzen:
Wer den Score von 1325 übertrifft und weniger als 2 Wochen benötigt, hat gewonnen 🙂
Nebenbei: Mein Ansatz war ein Local Search Ansatz und ich bin im Rahmen der «Kaffeepause», die bei uns den Abschluss eines spannenden aber auch anspruchsvollen Nachmittags bedeutete, nicht auf den gewünschten Score gekommen.
Zusammenfassen kann gesagt werden, dass beim Scoring die beste Lösung oft auch ein multiobjective Score sein kann. Bspw. mit einer «Pareto-front» zwischen Fairness & Wirtschaftlichkeit.
Für jedes Problem gibt es auch eine mathematische Lösung, wenn ich nur weiss, welches Ziel ich erreichen möchte.
Und zur Beruhigung für alle «Nichtmathematiker» oder für Menschen ohne Nobelpreis-Ambitionen:
Es ist oft nicht sinnvoll einen eigenen Algorithmus für ein Problem zu entwickeln. Für viele Problemlösungen gibt Standardformulierungen, die sinnvoll eingesetzt, den besten Nutzen-Ertrag bringen werden.
Unser Newsletter liefert dir brandaktuelle News, Insights aus unseren Studiengängen, inspirierende Tech- & Business-Events und spannende Job- und Projektausschreibungen, die die digitale Welt bewegen.